

中学2年生男子の生徒様とのやりとりです。
手先が器用でシャーペンを改造したものを見せてくれたり、手品を披露してくれたりします。
遊びたい盛り、面白い事大好き、中々勉強には気が乗らないかもしれません。
そんな中でもノートはきれいに書くという改善意識が定着し、だいぶきれいになりました。
やりだすと目標の時間まで頑張ってくれますので、次は習慣化ですね!
楽したい気持ちが人を進化させる
休校期間中、学校課題に加えて塾課題もやってくれていました。
那須:(ノート見せてもらい)おー、やってるね!
那須:(前回の塾の様子から)方程式、久しぶりにやって忘れてたところあったみたいだけど・・・?
生徒様:課題やって思い出しました!
中学生の数学で最も強い武器となる方程式。
ちゃんと解けていたはずのものが、時間が経って忘れている。
定着が甘かった部分があったかもしれません。
でも数式変形の考えはしっかりできていました。
方程式の感覚を思い出すのは容易だったようです。
多項式の加法と減法の予習をしました。
(3x+2)-(x-y+3)
=3x+2-x+y-3
=3x-x+y2-3
=2x+y-1
みたいな問題ですね。
この単元では「ひっ算」による加法と減法を行う問題も出題されます。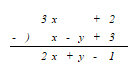
ひっ算にするとx同士、y同士が縦に並ぶので、同類項を習いたての2年生にとっては解きやすいと思うのですが、どうやっていいのかわからなくなる方もいます。
3x-x=2x
0-(-y)=y
+2-(+3)=-1
ここで項の理解ができているかどうかが問われるのかなと思います。
特に問題なく解き終わりました。
これで終わってしまっては、ちょっと学びとしてもったいない。
項の概念をよく理解できていることがわかったので、ちょっと応用的な話をしてみます。


(3x+2)-(x-y+3)
=3x+2-x+y-3
=(3x+2)+(-x+y-3)
ということを説明します。
「多項式の減法の計算では、引く式の符号を反転したものを足しても良い」
これを理解してもらいます。
すると、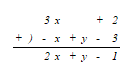
足し算で計算できるようになります。
どこまで簡単に感じるかは人それぞれですが、こちらの方が簡単に感じる方も多いです。

成功したかな?
これがわかると、連立方程式の計算にも応用できます。

楽したい気持ちは数学にとって重要です。
例えば解の公式が無ければ√が出てくる二次方程式を解くのは大変です。
公式に頼るのは好きではありませんが、使うべき公式はどんどん使って楽しましょう。
引き算よりも足し算の方が楽!
だから足し算にする!
楽のできる考え方なので、受け入れてもらいやすいです。


