
高校1年生男子の生徒様とのやりとりです。
cos(90-θ)の公式
cos(90-θ)の公式覚えていますか?
恐らく進学校の高校生と、一部の数学マニア以外、ほぼ覚えていないんじゃないかと思います。
それでいいと思います。
ちなみに進学校の高校生で覚えていなくても正しく計算できる方もいるかもしれません。
それはそれでOKです。
しかし、教科書を見ないとこれを計算できないというのはちょっとヤバイですね。
もちろん習いたてなら見ないとわからないかもしれません。
ただ、見ていてはなかなか見ずにできるようにはなりません。
見ないとわからない事が高校生になると増えてくるかもしれません。
そこで見てしまうと、「見ないとわからない病」に掛かるので、見た場合はできなかった問題としてできるようになるまで繰り返し演習しましょう。
今回生徒様は学校でまだ習う前の状態での予習です。
ですからそもそもこの公式を見たことすらなかったかもしれません。
もしかすると見ていたかもしれませんが、何故そうなるかの説明を受けたことはないでしょう。
ということで、その公式の理屈をお話ししました。
なお、この公式は覚えなくてもいいです。
でも教科書を見ずに計算できるようになりましょう!
図を書いて考える
教科書でも同じような説明ですが、こんな感じの図ですね。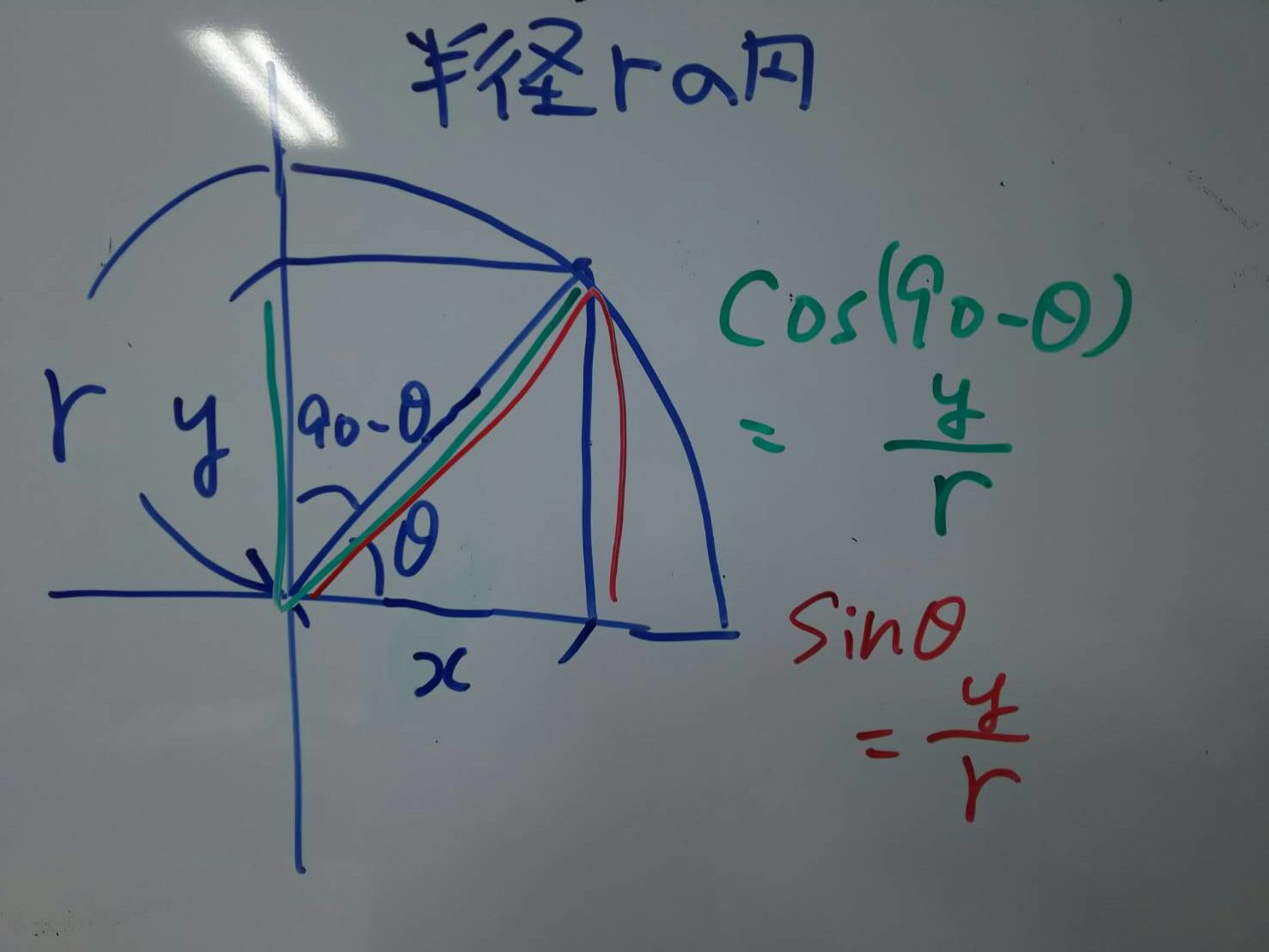
θにたいして、90-θがどの角になるのか。
cos(90-θ)がどの辺の比で、それがθであればどの辺の比なのか。
絵を描けば一目瞭然でしょう。
生徒様:なるほど
という感じで聞いてくれました。
公式の成り立ちを理解してくれたかと思います。
加法定理
ここからはやりとりの話ではありません。
高1では加法定理やっていませんからね。
知っていたかもしれませんが・・・。
これをおすすめする人を見たことはボクはあまりないですね。
でも、加法定理を使っても行けますし、意外と楽ですよ。
加法定理は次の公式です。
cos(α±β)=cosαcosβ∓sinαsinβ
「こっち覚えるくらいなら、cos(90-θ)の公式は覚える」というのはダメです。
数ⅡB取るなら、これは絶対覚えなきゃダメなやつです!
α=90、β=θとして使います。
cos(90-θ)
(=cos90cosθ+sin90sinθ)
=sinθ
「cos90出るからcos側消える」とか「cosの式なんだから、90-θで見る方変えればsinになるだろう」とか、そのあたりを考えて、()の計算を省略してしまって全然かまいません。
cos(90-θ)の公式もsin(180-θ)等の公式も、覚える必要ないですよね。
下手に覚えて符号間違えるよりも、その場で求めちゃった方が間違えないです。
ただ、「確かそんな公式あったなー」ということと、じゃあどうなるのかの求め方は覚えておいた方が良いですね。

