
中学3年生女子の生徒様とのやりとりです。
先入観
数学の試験で優秀な成績を収める生徒様に毎年聞かれる質問があります。
それはこんな問題です。
問.√5の整数部分をaとし、小数部分をbとする。このとき・・・
生徒様:整数部分と小数部分って何ですか?
これは言葉の意味から、どんなものかは想像がつきますよね。
√5=2.236…
という表記をしてもらうと、大体わかってもらえます。
生徒様:整数部分が5だから、aが5で・・・
生徒様:小数部分が.236…bは0.236…?
ここで√5が無理数ということが効いてきます。
延々と小数が循環することなく続いてしまいます。
このような「数」という表記方法では表せません。
これは一種の先入観じゃないかなと思います。
これは数学の成績とは強い相関を持っていないと考えています。
※どちらかと言うとクイズやパズル的な要素かなと。
那須:bの値がいくつになるという、「数」は書けないよね。
那須:でも、「数式」ならどう?
那須:つまり、足し算とか使っても良いってことだけど。
生徒様も「あ、なるほどー」というご様子に。
ルートが出てくるまで「値を求めなさい」みたいな問題は、大体1つの数に決まります。
※例外があるのですが、みんな自ずと使っているのに、その事には気付きにくいんですよね。
これが、ルートが出てくるとそうならないんですよね。
「0.236…」という数字は、√5の整数部分の2を取り除いた数です。
つまり、「√5-2」これがbなんですね。
実は似たことを既にやっている
さて、先ほどの例外の話です。
それは中学3年生でルートを習う前に出てくる無理数がヒントです。
そうです。
みんな大好き「π」ですね。
円に関する要素が入った図形の問題では、面積や体積にπが出てきます。
例えば(かなり適当ですが)こんな図形(正方形から扇形をくりぬいた図形)の面積ですね。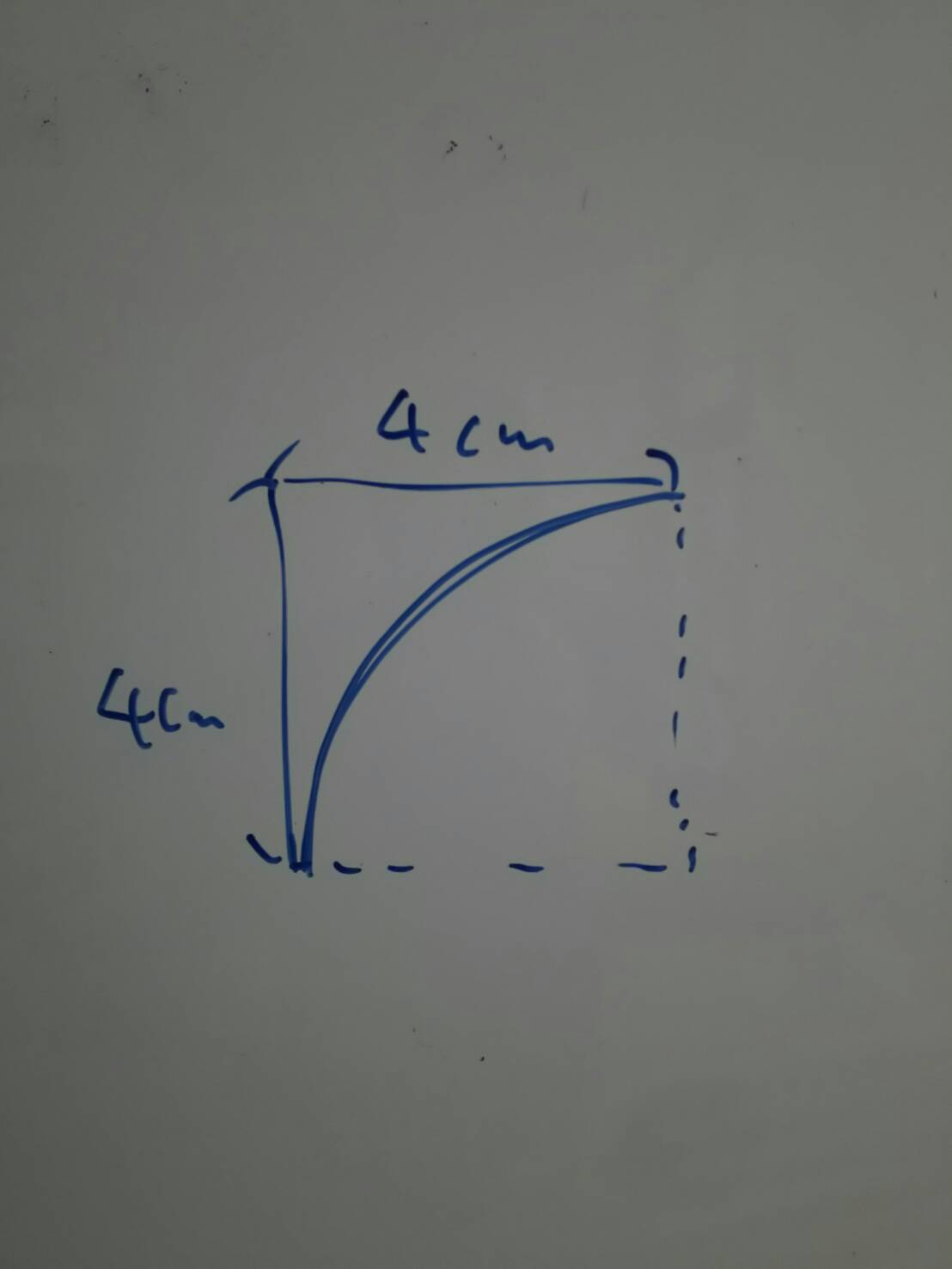
正方形の面積:4cm×4cm=16cm2
扇形の面積:4cm×4cm×π/4=4πcm2
求める面積:16cm2-4πcm2
無理数でこれ以上計算できないので、計算はここまでです。
ルートの小数部分と同じですね。

