
高校1年生男子の生徒様とのやりとりです。
生徒様のためにならない話
ボクは普段、あまり生徒様のためにならない話はしないよう心掛けています。
ブログをお読みの方、メールなどでやりとりさせて頂いた方はお分かりかと思いますが、ボクはかなり細かいです。
ですから、丁寧に説明しすぎて、生徒様の時間を無駄に奪ってしまう事を気にしています。
しかし、どうしても「あ、これ教えておいた方が良いな」と思うときが多いんですね。
それで生徒様が問題に正解していても声を掛けることがあります。
例えば、数学の「別解」です。
数学は色々な考え方があり、それぞれの考え方が正しければ答えにたどり着くという点が面白いと思っています。
そんな面白さを知ってもらいたいという思いがあり、色々なやり方を紹介します。
いろんなアイデアは問題を解くための手掛かりにもなります。
だから、無駄ではないと信じています。
少し経緯は違いますが、今回はそんなお話です。
※本題に入る前が既に長い・・・
無駄じゃないはず!
こんな問題があります。
コインを投げて表が出たらAが1点、裏が出たらBが1点とする。
この試行を繰り返し行い、3点を先に取った方が勝ちとする場合、勝敗の決まり方は何通りあるか。
例えば、表(1-0)、裏(1-1)、表(2-1)、表(3-1)となったら、Aが勝ちとなって勝敗が決まります。
生徒様はこれを「樹形図」を使って求めてくれました。
こんな感じのやつですね。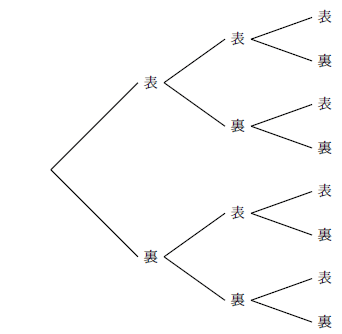
ただ、今回の問題は、「表裏表」、では勝敗がつかず、その表裏の出方によって最大で5回まで続きます。
試行回数が一定でないという点に難しさがあります。
とりあえず、樹形図を書けば答えがわかります。
ただ、全部書くと大変なので、「最初が裏」の場合は、「最初が表」の場合を表裏ひっくり返したものと思えば、ちょうど同じ通り数があることが分かります。
そういった工夫を施して数えてくれました。
樹形図は正しく絵が書ければ、正しい答えを導くことができます。
そのデメリットは「ちょっと面倒」な事です。
しかし、その面倒なことにしっかりと取り組めるかどうかは、大きな学力差になっていくでしょう。
ただ、式を使った計算ができるのであれば、それに越したこともありません。
那須:(あー・・・言いたい!)
生徒様が樹形図を書き、答え合わせにより正しい数字を確認後、その解説をします。
那須:うん、良いね!
那須:今回、Aが勝つ場合っていうのはさ、・・・
那須:だから場合分けをしてね、・・・
那須:1+3C1+4C2=1+3+6=10、だね。・・・

そうやって吸収したアイデアは、いずれ生徒様のためになるはずです。
那須:これはこの後にね・・・
生徒様:そんな難しい問題に・・・


無駄じゃないはず!
それが見たくて
新しいものに出会ったとき、生徒様方は本当にいい顔をしてくださいます。
「そんなもんか」でやっていた数学が「そんなやり方もあるのか!」と好奇心が刺激された瞬間です。
それがボクの1つのやりがいであり、それを見たくて色々試行錯誤しています。
これは言いたいことを言うための正当化ではありません!
※と言うとかえって怪しく聞こえてしまうかもしれませんが・・・

